Coupled Streamflow and Temperature Modeling for Aquatic Ecosystem Studies- Juniper Publishers

 

Juniper Publishers- Journal of Oceanography

Abstract

Many global aquatic ecosystems, particularly for those in high latitudes, are reported to be under pressure due to warming climate and anthropogenic interference. In this short article, we briefly discuss the two major environmental constraints for an aquatic ecosystem-streamflow and stream temperature, which haven't received enough attention thus with only sparsely available concurrent in-situ measurements across the globe. A novel numerical solution, i.e., the Dominant River-Tracing-based streamflow and Temperature (DRTT) model, is introduced, and it has been developed for the simulations of both daily streamflow and temperature along entire drainage networks for large regions, filling the data gap usually faced by aquatic ecologists. The DRTT model has been successfully applied in the study of freshwater salmon habitat and associated productivity in 1500 North Pacific Rim rivers. However, that study also indicated big challenges in the model calibration due to the lack of observations, and the high complexity and nonlinearity in model structure and processes. Opinions on how to effectively tackle such challenges are discussed in the latter part of the article.

Streamflow, Water Temperature and Aquatic Ecosystem

Aquatic ecosystem is a dynamic system that a community of aquatic organisms live and interact within water environments. The ecological services provided by aquatic systems are well- recognized, and they are including replenishment and purification of water, buffers from flooding, drought and wildfire, and providing wildlife habitats [1]. However, the abundance and distribution of aquatic ecosystems become increasingly vulnerable due to the increase of global temperature and higher intensity of human activities [2]. Ocean aquatic ecosystems are more susceptible to losses of deep sea biodiversity, fish populations and shorelines, while freshwater ecosystems are more threatened by land use change, eutrophication, overexploitation, hydrological disturbance and invasive species [3].

Over the past two decades, the change of climate and environment due to anthropogenic activities have drawn more attention to researchers due to their great impacts on aquatic ecosystem. For those studies, a variety of hydrological, meteorological and water environmental indices were introduced to assess the impacts of climate change and anthropogenic pressures on aquatic ecosystems. Streamflow and temperature are among the most significant parameters casting crucial environmental constraints on the availability, quality, distribution, and range of habitats [4]. Specifically, the magnitude and variability of streamflow are fundamentally crucial to the behavioral responses and life stages of numerous aquatic species, whereas stream temperature has a decisive influence on organism growth and distribution, influencing the metabolic rates , spawning and the timing of migration [4]. Moreover, streamflow and water temperature influence water quality in a lot of aspects and are very sensitive to physical conditions of freshwater ecosystems [5]. This suggests that the state of entire aquatic ecosystem can be studied by streamflow and temperature conditions.

Development and Applications of the Coupled Streamflow and Temperature Model

Unfortunately, streamflow and temperature observations from stream gauge networks are often sparsely distributed, without enough information to characterize the study region, false conclusions can be drawn for further aquatic ecosystem research. Thus, efforts to model the streamflow and temperature in continuous and discrete space, have resulted. Multiple attempts have been made to the development of distributed hydrologic models to predict streamflow, for example, Variable Infiltration Capacity (VIC) model [6] and Soil and Water Assessment Tool (SWAT) model [7]. Gridded rainfall and air temperature forcings interpolated from regional meteorological stations are employed in the distributed hydrologic models, and streamflow can be simulated continuously for each grid point of the study basin [4]. However, simulations of water temperature are often constrained to streams in specific reaches or smaller, nested sub-basins. A semi-Lagrangian water temperature model for advection-dominated river systems, is applied to assessing climate change impacts on a tributary of the Snake River of America with a drainage area of 24,800km2 [8]. However, spatial and temporal patterns of interactions between streamflow and stream temperature over large regions was rarely studied [4].

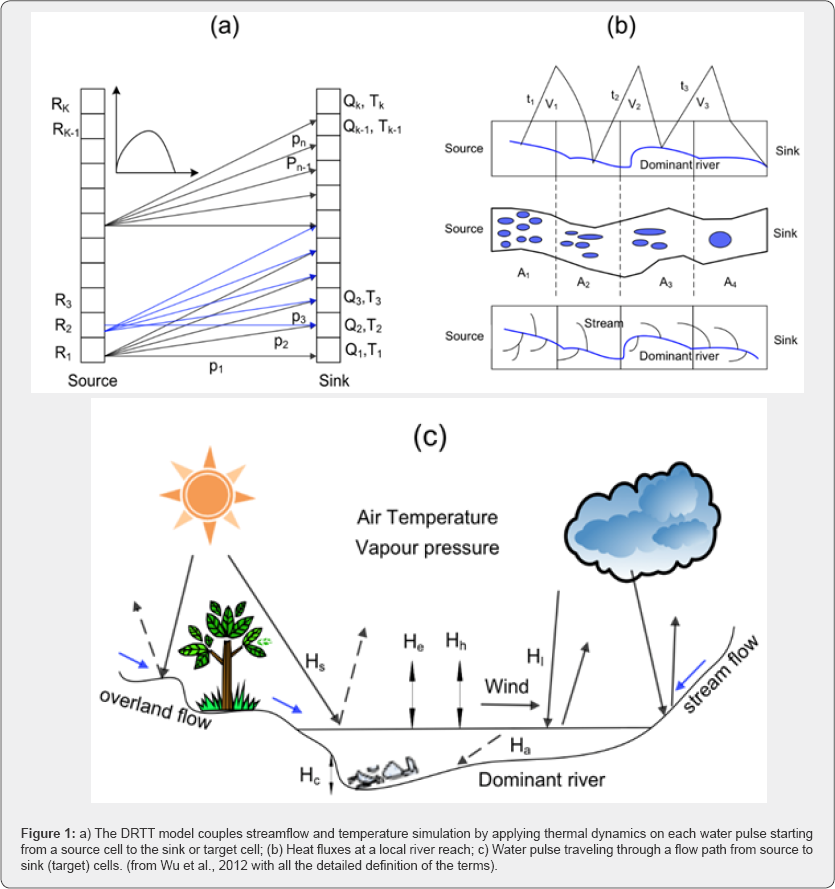
To obtain improved simulations of both daily streamflow and temperatures along entire drainage networks, Wu et al. [4] developed a dominant river-tracing-based streamflow and temperature (DRTT) model and applied the coupled model using daily runoff inputs from a macroscale hydrological model to determine historical and potential future streamflow and temperature conditions simultaneously in Pacific Northwest [4]. A source-sink hydrologic routing model was first employed within the DRTT model to distribute the daily runoff estimates and predict streamflow for every grid cell along defined basin flow pathways, and stream thermal dynamics simulations are then coupled to the DRTT model to estimate water temperature (Figure 1) [4]. The study by Wu et al. [4] using coupled streamflow and temperature model suggests that the projected climate change will have great impacts on snow dominant streams with lower summer streamflow and warmer summer stream temperature, and further increase summertime thermal stress for cold-water fishes in Pacific Northwest [4,9].

Seeking the Best Model Performance with Optimized Parameterization

Physically-based models generally use interconnected mathematical functions with a number of parameters based on the laws of conservation of mass, momentum and energy as a simplified representation of the underlying physical system [10]. Some parameters can be measured in the laboratory or in the field, while many of the parameters, which are not fully physical, can only be estimated based on available data [11]. Model calibration, either automatic or manually, refers to the process of determining the unknown parameters of a dynamic mathematic model that best fit observation data, which is also called parameter estimation, data fitting [12]. It is assumed that the calibrated model can provide adequate justification for the prediction and decisionmaking purposes. However, the physically based coupled model is often highly complex and formulated by nonlinear, dynamic, stochastic partial and ordinary differential equations. This complex nonlinearities may lead to non-convexity, which means several local minima in the area of interest can be obtained in the optimization problem and parameter solution sets with equivalent calibration performance can be reached [13]. It is even more challenging when the coupled model is distributed rather than lumped, due to the computational burden and inadequate observations in both spatial and temporal scale [14]. However, thanks to the advances in computing power and additional observations from remote sensing, automatic optimization algorithms have been successfully adopted in calibrating models to some extent.

The definition of the optimum model parameter set depends primarily on several factors, such as the quality and the quantity of observations, the simplicity of model structure, the efficiency of the optimization algorithm, and the definition of objective functions used in the optimization procedure. In the absence of adequate constraints to unknown parameters in the physically based coupled streamflow and temperature model, researchers should focus on collecting more detailed and accurate spatially distributed observations for model calibration process. For example, remote sensing of evapotranspiration, infiltration, and snowmelt data can be used in the calibration process rather than relies solely on approximating observed discharges. Furthermore, remote sensing data of rainfall, land surface temperature can also be employed in the study basin when meteorological stations are too spare. It is worth to mention that, for aquatic ecosystem studies for ungauged basins, the estimation of unknown parameters should not be solely based on automatic optimization techniques, but also modelers' own experiences.

For more about Juniper Publishers please click on: https://twitter.com/Juniper_publish

For more about Oceanography & Fisheries please click on: https://juniperpublishers.com/ofoaj/index.php