A test for Costs Subadditivity in the Fishery Sector- Juniper Publishers

 

Juniper Publishers- Journal of Oceanography

Abstract

The seminal work by Baumol et al. [1] has highlighted the importance of analyzing firms' costs structure. This allows to design proper policy measures and to understand the impacts of those policies in markets. The note presents an original method and an application for testing costs subadditivity in the fishery sector, by using a system of supply functions under strict conditions and assumptions. The method is practical, though robust, and can be appied in the absence of detailed data on costs structures. Under stringent hypothesis (that delimit the application) they can be inferred from the supply functions. Subadditivity in costs, in fact, is a more proper economic definition (and methodological approach) than traditional economies of scale in fishery. The latter, in fact, does not depend from the vessel technology, but on the degree of quantity and variety of fish species in the ocean.

Introduction

Fishery vessels are multiproduct firms. The multiproduct firm's structures of costs and technology are important determinants of multiproduct industry structure. The seminal work by Baumol, Panzar & Willig [1] has established theoretical conditions for the existence of multiproduct cost advantages that can be achieved by specialized or diversified firms according to the scale and scope of their production. The concept of cost subadditivity provides an additional measure by which to characterize the multiproduct cost structure. Costs subadditivity is a property that characterize production costs. It implies that production from only one firm is socially less expensive (in terms of average costs) than production of a fraction of the original quantity by an equal number of firms. Investigating the existence of costs subadditivity (or superadditivity) is not (only) an academic exercise but can provide important hints for policy guidance. In fact, a vessel with super-additive costs can save money by braking itself into two or more divisions. Most probably, unless there are factors that preclude such decentralization, we would not expect to observe profit-maximizing firms operating at super-additive costs. In that case, subsidies could be awarded in order to minimize the vessel losses, when the "main" problems should be diagnosed at the cost function level, and the "consequential" measure be taken at that level. On the contrary, a firm with subadditive costs, may enjoy cost advantage that [1] either make subsidies inefficient or improper, [2] or render any kind of antitrust policy absolutely not apt, if the firm enjoys dominant positions due to efficient production that is represented by costs subadditivity. Such analysis can also apply to tackle the effects of policies that impact costs of production inputs, including labour, as in the case of the landing obligation [3].

It is also important to highlight that subadditivity in costsis a more proper economic definition (and methodological approach) than traditional economies of scale in fishery. The latter, in fact, does not depend from the vessel (firm) technology, but on the degree of quantity and variety of fish species in the ocean.

Formally, a cost function is said to be subadditive at an output vector, say q, if and only if it is cheaper for a single firm to produce q than to split it among more than one firm in any fashion. In formal terms: the function c(q) is subadditive at the output level “q if and only if c('q)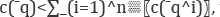 where non-negative “q^i are that

In the case of fishery, for instance the possibility to fish different species with the same device mostly depends on the sea productivity and variety of species. This allows, a "savings" in the costs, e.g. costs subadditivity. According to Baumol et al. [1], in the theory of contestable markets, costs subadditivity might favor a market structure characterized by few firms operating in the sector (natural oligopoly and natural monopoly).

This means that the current technology allows multiproduction (e.g. simultaneously fishing different species with the same net or trawl) at a lower cost than separate production of each output that is multi-produced. In this perspective, total costs are lower than in the case the vessel had to use a different device for every type of species. Economies of scope exist if the costs of producing each product separately exceed the costs of producing all products jointly. Economies of scope and declining average incremental cost for each product are sufficient conditions for subadditivity. The presence of cost subadditivity would suggest that some form of fishermen's monopoly is appropriate on private efficiency grounds. The monopoly could be private, or could entail complete government ownership and control, or could include extensive government coordination and regulation as is found in north, or could consist of a set of single-product firms contracting among themselves [4].

The note presents an original method for testing costs subadditivity in the fishery sector, by using a system of supply functions under strict conditions and assumptions. The method is practical, though robust, and can be applied in the absence of detailed data on costs structures. Under stringent hypothesis (that delimit the application) they can be inferred from the supply functions.

The note is organized as follows: section 2 presents a survey of the (scarce) economic and econometric literature that has produced test for subadditivity in industries. Section 3 presents an original methodology, by developing testable implications and testable empirical specifications, under stringent conditions.

Tests of Cost subadditivity: a Survey of the Literature

Tests of cost subadditivity are difficult to devise, since one of the requirements is global knowledge of the cost function, while local knowledge in the neighborhood of the point of approximation is usually the best that can be achieved. Acceptance of local subadditivity then provides a sufficient condition for global cost subadditivity [5]. Although Baumol et al. [1] provide both necessary and sufficient conditions for cost subadditivity, the long-run multiproduct cost function allows only local sufficient conditions. Failure to establish cost subadditivity will then not preclude its existence. Tests of cost subadditivity specify all factors of production to be in full static equilibrium and outputs as exogenously fixed. In general, cost subadditivity requires economies from proportional expansion of the product vector along an output ray and economies arising from product combinations along a cross-sectional hyperplane[1].

The Evans-Heckman [5] test for subadditivity implies a two-product industry where all firms have access to the same technology. The cost function C(q1, q2) is locally subadditive at

With i = 1 n.

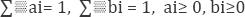
For at least two ai and bi not equal to zero. The test computes (2) for an admissible range of outputs and allows for local subadditivity. The degree of subadditivity can be measures as:

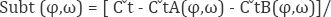
Where φ and ω are parameters that satisfy 0 ≤ φ ≤ 1 and 0 ≤ ω ≤ 1. If Subt (φ,wω) is less than zero, the cost function is subadditive with respect to the industry configuration at the selected time t. If Subt (φ,ω) equals zero the cost function is additive; if it is larger than zero the cost function is superadditive.

Another (indirect) way to test for subadditivity, is looking at the existence of economies of scope in the industry. Scope economies (diseconomies) are reflected into cost savings (cost disadvantages) associated with the joint production of many outputs. Economies of scope exist if the costs of producing each product separately exceed the costs of producing all product jointly. Economies of scope and declining average incremental cost for each product are sufficient conditions for subadditivity. The average incremental cost of output i, when the total output vector is q~, is the cost of producing out vector q~, minus the cost of producing all of q~ excludingproduct i, divided by the output of i, q'i. [5]. Scope economies are a necessary (but not sufficient condition) for costs subadditivity.

Suppose that the multi-product cost function is represented by C = C (q; w) where q = (q1, q2, q3) is the quantity of three different outputs and w = (wL, wk, wF)are respectively the prices of labor, capital and other inputs. Local measures of global and product-specific scale and scope economies can be easily defined. The measure of global or aggregate scope economies for our three-output case can be computed as:

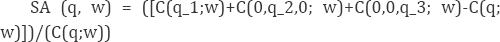
with SCA> 0 (< 0) denoting global economies (diseconomies) of scope.

Product-specific economies of scope for output i are

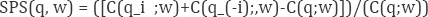
where C(qi; w) is the cost of producing only output i, and Si >0 (<0) indicates a cost disadvantage (advantage) in the "standalone" production of output i.

Vessels as Multiproduct firms: a Tentative Test for Subadditivity in Fishery Production

Vessels can be considered as multi-product firms because they can fish a variety of species (given the sea productivity) with the use of the same technology and capacity. This allows in saving on costs, and might imply costs subadditivity. The individual vessel multi-product supply curve is:

where qn, is the quantity of n species caught and sold by the vessel; cn, are the vessel's production costs and on pn, the market price for n types of caught species. Vessels are price-takers and price at marginal cost. Therefore, the supply function is also the cost function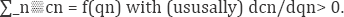

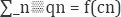
Given, c(qn) =p(qn) the supply function ithe supply function is ^

The assumption of marginal cost pricing is required to fully exogenize prices and costs and keep multi-product quantities as only control variable. Such assumption is grounded on the evidence that fish prices are determined by the market (no collusion among firms) and are pretty similar among all vessels. Given the above assumptions, our exercise implies two steps [69].

Step 1 We empirically estimate a system of supply functions (which are also the costs functions) for n different products. Required data are produced quantity for each n species and related price for each species [3].

Step 2 Recalling that a cost function c(q) is subadditive at the outfut level^-q if and only if 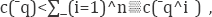, where non-negative ^-q^ Aiare that 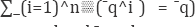then there is costs subadditivity at the output level “q, where a perfect competition market-defined price if and only if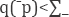 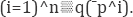As necessary condition, when estimated parameter for quantity/quantities present negative estimated sign then we can assume costs subadditivity [3] at certain output level. An increase in prices/costs might generate a corresponding decrease in output quantities, in the relationship described by the supply function, which usually imply a positive relationship price/cost/produced quantity. This can be interpreted as a symptom of costs subadditivity. If detailed data on costs are available the usual Evans-Heckman test can be applied.

Conclusion

The note presents an original method for testing costs subadditivity in the fishery sector, by using a system of supply functions under strict conditions and assumptions. The method is practical, though robust, and can be applied in the absence of detailed data on costs structures. Under stringent hypothesis (that delimit the application) they can be inferred from the supply functions. The method can have important policy implications. Analyzing the structure of the firms' costs allows to design proper policy measures and to understand the impacts of those policies in markets (Appendix 1).

Appendix

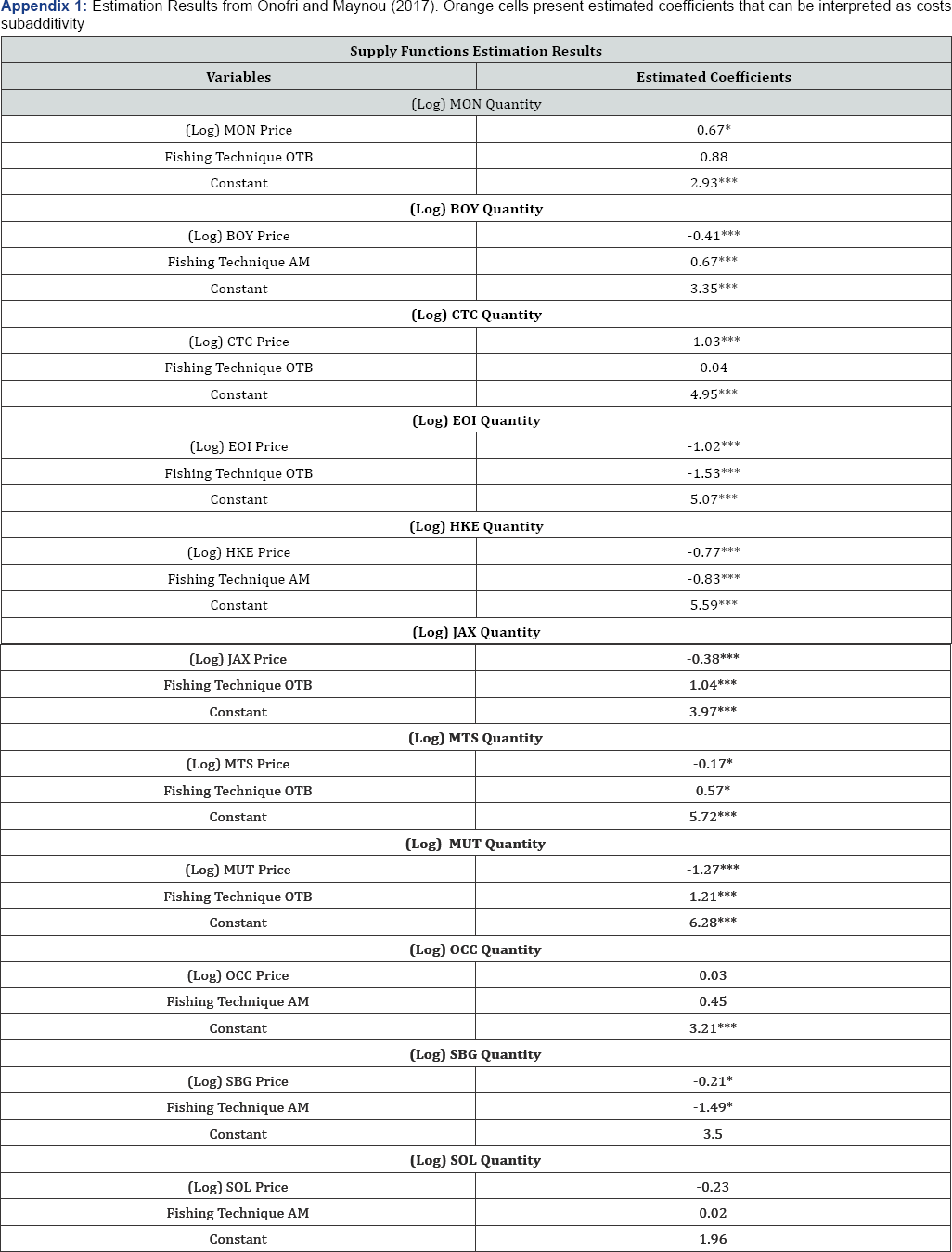
*= 10% statistically significant; **= 5% statistically significant; ***= 1% statistically significant. FAO 3-alpha code (MON: Monkfish; EOI: White octopus; HKE: European hake; JAX: Horse mackerel; MTS: Mantis shrimp; MUT: Red mullet; SQM: Squid; BOY: Purple murex; CTC: Cuttlefish; OCC: Common octopus; SAN: Sand eel; SBG: Golden seabream; SOL: European sole).

To Know More About Journal of Oceanography Please Click on: https://juniperpublishers.com/ofoaj/index.php