Wind-Wave Relation during Hurricane Matthew in 2016: Buoy Measurements and Applications- Juniper Publishers

                  Juniper Publishers- Journal of Oceanography

Abstract

Analysis of wind and wave parameters measured by a data buoy during Hurricane Matthew in October 2016 indicates that the dimensionless wave height and period are approximately linearly related. It is found that, under the conditions of growing wind seas and aerodynamically rough flow over the ocean U10= 36 HS/LP here U10 is the wind speed at 10m, H5 is the significant wave height and TP is the dominant wave period. Further verifications of this relation are successful during Hurricanes Dean in the Caribbean Sea, Katrina in the Gulf of Mexico, Estelle near Hawaii and Typhoon Russ near Guam in the Pacific. In addition, when the variation of TP is small and Hs may be linearly related to the wind speed. A formula is proposed using Matthew's growing wind seas as an example. These formulas may be useful in applied oceanography and fishery sciences and management.

Introduction

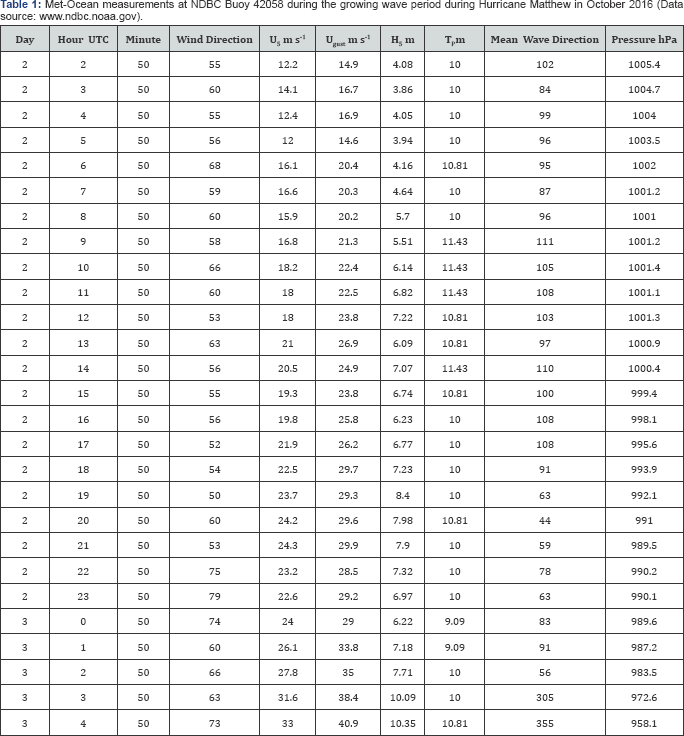
In oceanography and fishery, operational formulas for wind and wave interaction are needed, particularly under tropical cyclone conditions. Simultaneous meteorological-oceanographic (met-ocean) measurements of the wind speed at 5m, US , significant wave height, HS and dominant wave period, TP were made in October 2016 by the National Data Buoy Center (www.ndbc.noaa.gov) at NDBC Buoy Stations 42058 near the storm track for Hurricane Matthew over the Central Caribbean Sea (for buoy location and datasets, see www.nhc.noaa.gov and for the hurricane track, (see www.ndbc.noaa. gov). These datasets are listed in Table 1. The purpose of this research note is to investigate the relations among these 3 parameters.

Criteria for the wind sea

In order to minimize the effects of swell, conditions under the wind sea are investigated and acquired first. According to Drennan et al. [1], a wind sea is defined when

HS/ LP ≥ 0.020.............. (1)

Lp = (g/2n) Tp2 =1.56Tp2................ (2)

Here LP is the dominant wave length in meters and g is the gravitational acceleration

(=9.8ms-2). Note that the parameter HS/ LP is called wave steepness, which is available from routine buoy measurements.

Adjusting the wind speed from 5 to 10m

Because the wind speeds were recorded at 5-m instead of the standard 10-m during Matthew in 2016, one needs to adjust U5 to U10 using the power-law wind profile [2] that

U10 / U5=(10/5)p.............. (3)

Here P=(Ugust/U-1)/2=(G-1)/2 , where G is the gust factor and Ugust is the wind gust measured at the buoy [2].

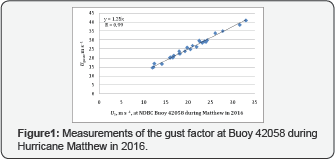
Figure 1 shows that G=1.25 so that p=0.125 with a very high correlation coefficient (R=0.99). Substituting this p value into Eq. (3), we have,

U10 = 1.1 U5............ (4)

Using Eq. (4), we can now adjust the wind speed from 5 to 10m.

Relation between wind and wave parameters

gH5/U210 , and wave period, gTp/U10 are often related according to a power law that, e.g., Hsu et al. [3],

gh5/U2i0=a(gTp/U10)b............... (5)

Here coefficients "a" and "b" need to be determined from experiments.

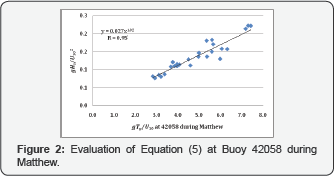
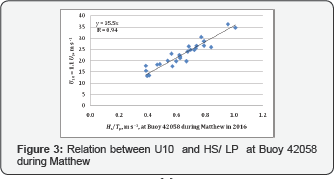
According to Andreas et al. [4], for aerodynamically rough flow over the ocean, needs to be greater than 9ms-1. Using these criteria for the wind speed and the onset of wind seas provided in Eq. (1), datasets for Hurricane Matthew in 2016 (Table 1) are analyzed according to Equations (4) and (5). Figure 2 shows that the exponent "b" is approximately unity, indicating that the dimensionless wave height and its period are approximately linearly related. Therefore, if we set b=1 in Eq. (5), one gets following equation based on Figure 3.

Ul0 = 36Hs / Tp............... (6)

As indicated in Table 1, when the variation of is small, and may be correlated linearly so that,

H = cU10 + d ..........(7a)

Here c and d need to be determined by field experiments.

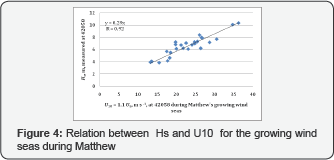
As shown in Figure 4, Eq. (7a) becomes

Hs = 0.29U10 ------------(7b)

This equation states that the significant wave height is about 30% of the wind speed. This 30% rule of thumb may be useful in operational oceanography and fishery management. Note that the coefficients in Equations (7a) and (7b) may vary depending on different met-ocean conditions.

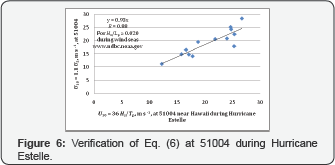
Now, in order to further verify Eq. (6), pertinent datasets from 3 other NDBC buoys are employed: they are: 42059 in the eastern Caribbean during Hurricane Dean in 2007, 51004 located near Hawaii during Hurricane Estelle in 1986, and 52009 near Guam in the western Pacific during Typhoon Russ in 1990. For buoy locations and datasets for these tropical cyclones, see www.ndbc.noaa.gov; for tracks of Dean and Estelle, see www. nhc.noaa.gov, and for Typhoon Russ, see www.usno.navy.mil/ JTWC/.

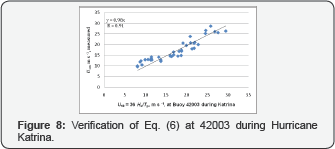
Using Eq. (4) and simultaneous measurements of US Hs and T at 42059 for Dean, 51004 for Estelle and 52009 for Russ, our results are presented in Figure 5-7. In addition, from 15 UTC on 26th thru 05 UTC on 28th in August 2005, U10 Hs and Tp were measured at NDBC Buoy 42003 located on the right side of the storm’s track during this period when Eq.(1) was valid (see http://www.ndbc.noaa.gov/hurricanes/2005/katrina/), Eq. (6) is further verified as presented in Figure 8. If one accepts these high correlation coefficients (R >0.88) as indicated in these figures, Eq. (6) should be useful in fishery sciences and managements. Note that, since the slopes in these figures are higher than 0.93, they are within the 90 % of composite field accuracy of wind speed measurements set by the NDBC.

Conclusion

On the basis of aforementioned analysis and discussions, it is concluded that

(1) Simultaneous measurements of wind and wave parameters during Hurricane Matthew in 2016 indicate that the dimensionless wave height and period are approximately linearly related during growing wind seas for the wind speeds higher than 9m s-1 .
(2) A relation between wind and wave parameter is proposed as presented in Eq. (6), which is further verified using 4 other buoys during one typhoon and 3 other hurricanes. These results may be useful in applied oceanography and fishery sciences and management and
(3) When the variation of wave period is small during the growing wind seas, it is possible to correlate the wind speed and significant wave height directly. A formula is proposed (Eq. 7) for operational oceanography and fishery management.
To Know More About Journal of Oceanography Please Click on: https://juniperpublishers.com/ofoaj/index.php
To Know More About Open Access Journals Publishers Please Click on: Juniper Publishers